About Machine Learning ( Part 1: Gradient Descent )

Data Science

Target Variable

The target variable is the variable the model aims to predict or explain. It’s also called the dependent variable or label.

Attributes

Attributes are the features or variables that describe each instance in a dataset. They are also known as features, columns, or independent variables.

Instances

Instances represent individual samples or data points in a dataset. They are also referred to as samples, rows, or observations.

Design of Experiments

Strategy of Experiments

1. Best Guess Appraoch
2. One-Factor-at-a-time: Standard practice but not efficient; Does not consider interactions.
3. Factorial Design: Considers Interactions; Is more efficient.

Principles

1. Randomization: Conducting experiments in a random order to mitigate systematic bias.
2. Replication: Repeat experiments to estimate error and improve precision. (* not the same as measurement error)
3. Blocking: Include experimental factors to mitigate variance from nuisance factors.

Public Data Repositories

• Federated Research Data Repository
• UCI Machine learning Repository

Optimization

Making the best or most effective use of a situation or resource. In terms of mathematics, we call this reducing a Cost Function (a.k.the objective function)

J(θ) =?

We can use optimization to minimize the overall error ( linear model ):

$$
J(m, b) = \sum_{i=0}^{N} [x_i - (mx_i + b)]
$$

A solution is referred to global or local maximum or minimum. Mean Squared Error:

$$
\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
$$

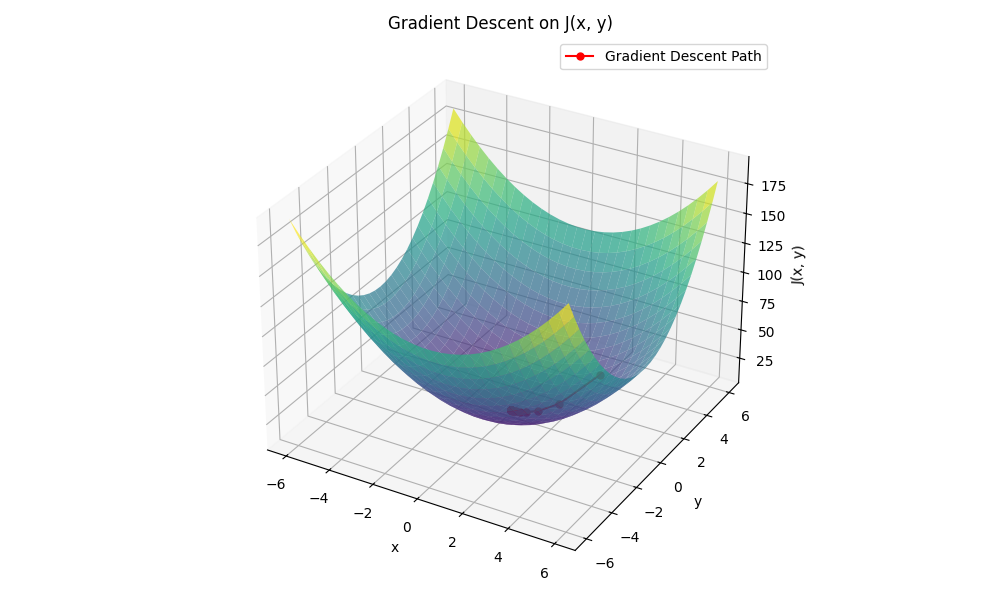
Gradient Descent

1. Guess the initial values of the problem parameters (x, y)
2. Calculate the value of the objective function
3. Determine the Gradient of the function
4. Change the parameters of the objective function slightly in the direction of the gradient
5. Repeat until the error is close to zero or some terminating condition is met.

Example

https://github.com/kongchenglc/Machine-Learning-Examples

Problems with Gradient Descent

• High dimensional Data is challenging
• Only good for Strictly Convex Objective Functions
• Requires a lot of memory occupancy

Alternatives to Gradient Descent

A solution is referred to global or local maximum or minimum ( Non linear methods… Non convex )

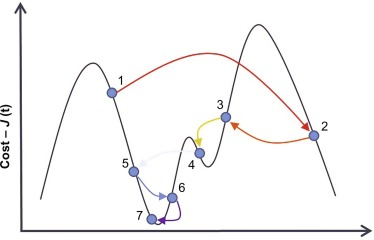
1. Simulated Annealing

Key Features of Simulated Annealing:

1. Global Search Capability:

   • Simulated Annealing can escape local optima due to its ability to accept worse solutions $\Delta f \geq 0$ at high temperatures.
   • As the temperature decreases, the algorithm becomes more “greedy,” eventually converging to a global or near-global optimum.

2. Probabilistic Acceptance Rule:

   • The acceptance of worse solutions is governed by the probability function $ P = e^{-\Delta f / T} $.
   • This allows the algorithm to explore the solution space freely during the initial stages, avoiding premature convergence.

3. Wide Applicability:

   • Simulated Annealing does not rely on specific properties of the objective function, such as differentiability or continuity.
   • It is suitable for both discrete and continuous optimization problems.

Advantages and Disadvantages of Simulated Annealing:

Advantages:

• Simple to implement and widely applicable.
• Capable of avoiding local optima.
• Does not require the objective function to be differentiable or continuous.

Disadvantages:

• Computationally intensive, especially for large-scale problems, as it may require many iterations.
• Convergence is slow, and performance heavily depends on parameters like initial temperature and cooling rate.
• In some cases, it may fail to find the true global optimum, instead settling on a near-optimal solution.

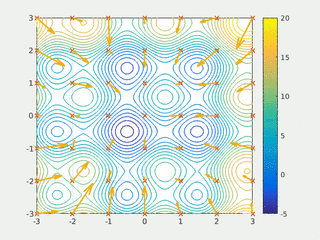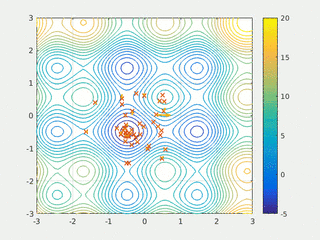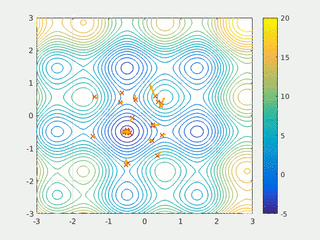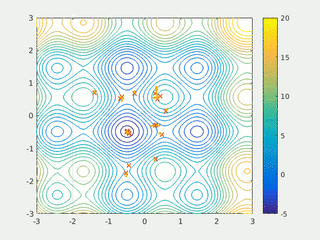
2. Particle Swarm Optimization

Main Features:

• Inspired by Nature: It simulates the social behavior of birds flocking or fish schooling, where each particle adjusts its position based on personal and collective experience.

• Velocity and Position Updates: Each particle updates its position based on its best solution and the best solution found by the group.

• Population-Based: PSO uses a group of particles (potential solutions) to explore the solution space.

Advantages:

• Simple and Easy to Implement: PSO has fewer parameters compared to other algorithms like Genetic Algorithms.
• Global Search: PSO can escape local optima, helping it find a better global optimum.
• No Gradient Needed: It does not require derivative information, making it suitable for complex, non-differentiable problems.
• Flexible: It can be applied to both continuous and discrete optimization problems.

Disadvantages:

• Slow Convergence: PSO can take a long time to converge, especially for complex problems.
• Parameter Sensitivity: The performance heavily depends on the selection of parameters like inertia weight and acceleration coefficients.
• Premature Convergence: In some cases, PSO may converge prematurely to a suboptimal solution.

PSO is widely used in optimization problems where derivative information is unavailable or expensive to compute, with the trade-off being a potential slower convergence or suboptimal solutions in complex scenarios.

3. Genetic Algorithms

Key Features:

1. Population-Based Search: GA maintains a population of potential solutions, enhancing its ability to explore the solution space globally.
2. Incorporates Evolutionary Concepts: Inspired by natural selection, it uses operators like selection, crossover, and mutation.
3. Global Search Capability: Can escape local optima by introducing randomness through crossover and mutation.
4. Fitness Evaluation: Solutions are evaluated using a fitness function, which guides the evolution toward optimal solutions.
5. Flexible Objective Function: GA works on a wide range of optimization problems without requiring derivative information.

Advantages:

1. Global Optimization: Effective at finding global or near-global optima, especially in non-convex problems with multiple local optima.
2. Flexible and Robust: Can handle complex, non-linear, and multi-modal objective functions.
3. No Requirement for Gradient Information: Suitable for optimization problems where derivatives are unavailable or undefined.
4. Adaptability: Easily adaptable to various problem domains, including discrete and continuous optimization.
5. Diverse Exploration: Maintains a diverse population, reducing the risk of premature convergence.

Disadvantages:

1. High Computational Cost: Requires significant computational resources, especially for large populations or complex fitness evaluations.
2. Parameter Sensitivity: Performance heavily depends on proper tuning of parameters like mutation rate, crossover rate, and population size.
3. No Guarantee of Global Optimality: May converge to a suboptimal solution, particularly if not run for enough generations or with improper settings.
4. Randomness Dependency: Relies on stochastic processes, leading to non-deterministic results.
5. Slow Convergence: Compared to deterministic methods, GA can be slower, especially for problems with a clear gradient or simpler structure.