Transformer ( Part 1: Word Embedding )

Word Embedding is one of the most fundamental techniques in Natural Language Processing (NLP). It represents words as continuous vectors in a high-dimensional space, capturing semantic relationships between them.

Why Do We Need Word Embeddings?

Before word embeddings, one common method to represent words was One-Hot Encoding. In this approach, each word is represented as a high-dimensional sparse vector.

For example, if our vocabulary has 10,000 words, we encode each word as:
$$
\text{dog} = [0, 1, 0, 0, \dots, 0]
$$
However, this method has significant drawbacks:

1. High dimensionality – A large vocabulary results in enormous vectors.
2. No semantic similarity – “dog” and “cat” are conceptually related, but their one-hot vectors are completely different.

Word embeddings solve these issues by learning low-dimensional, dense representations that encode semantic relationships between words.

---

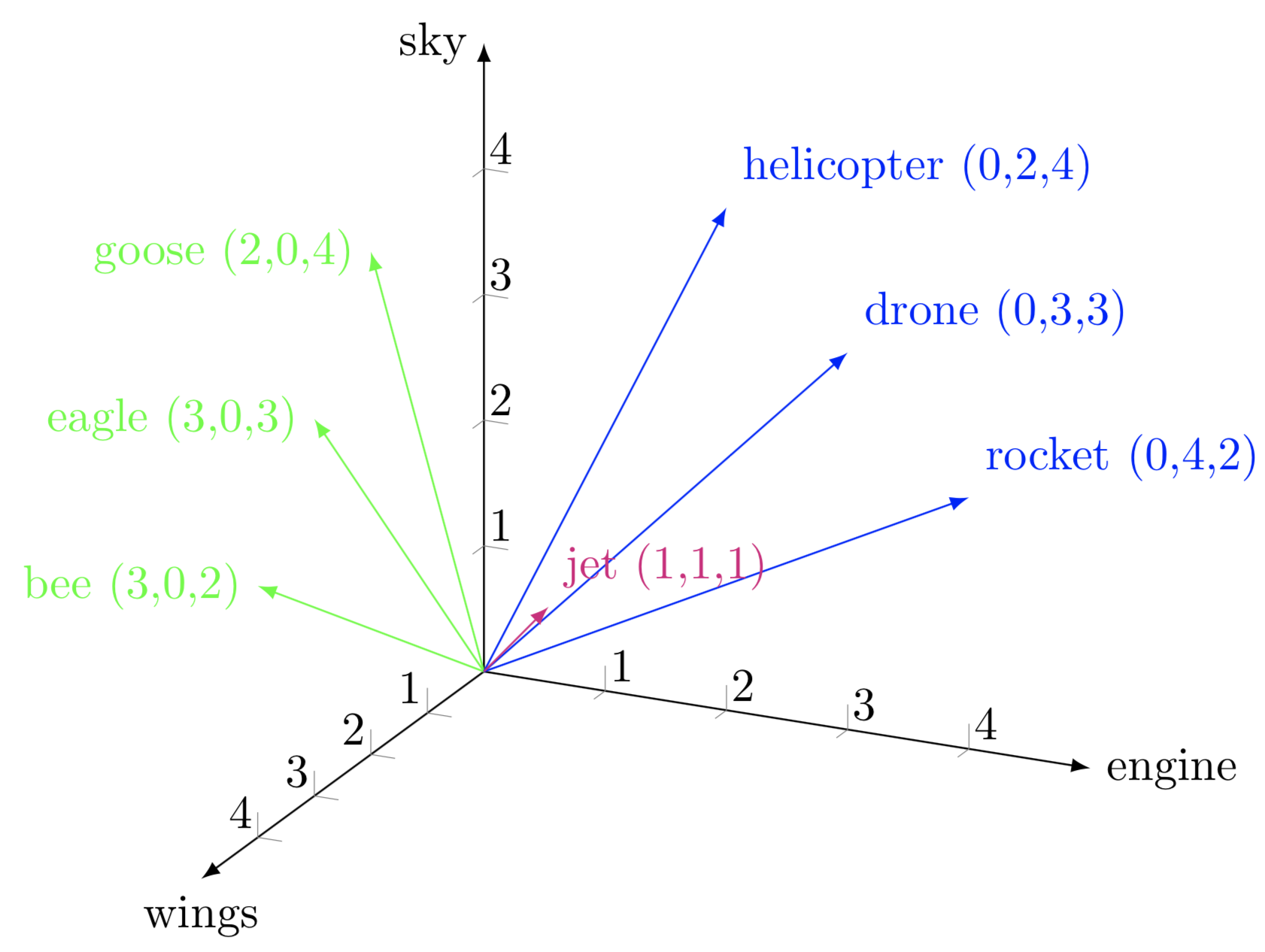
Word Embeddings and Dot Product: A Geometric Perspective

Word embeddings map words into a vector space, where semantically similar words are placed close to each other.

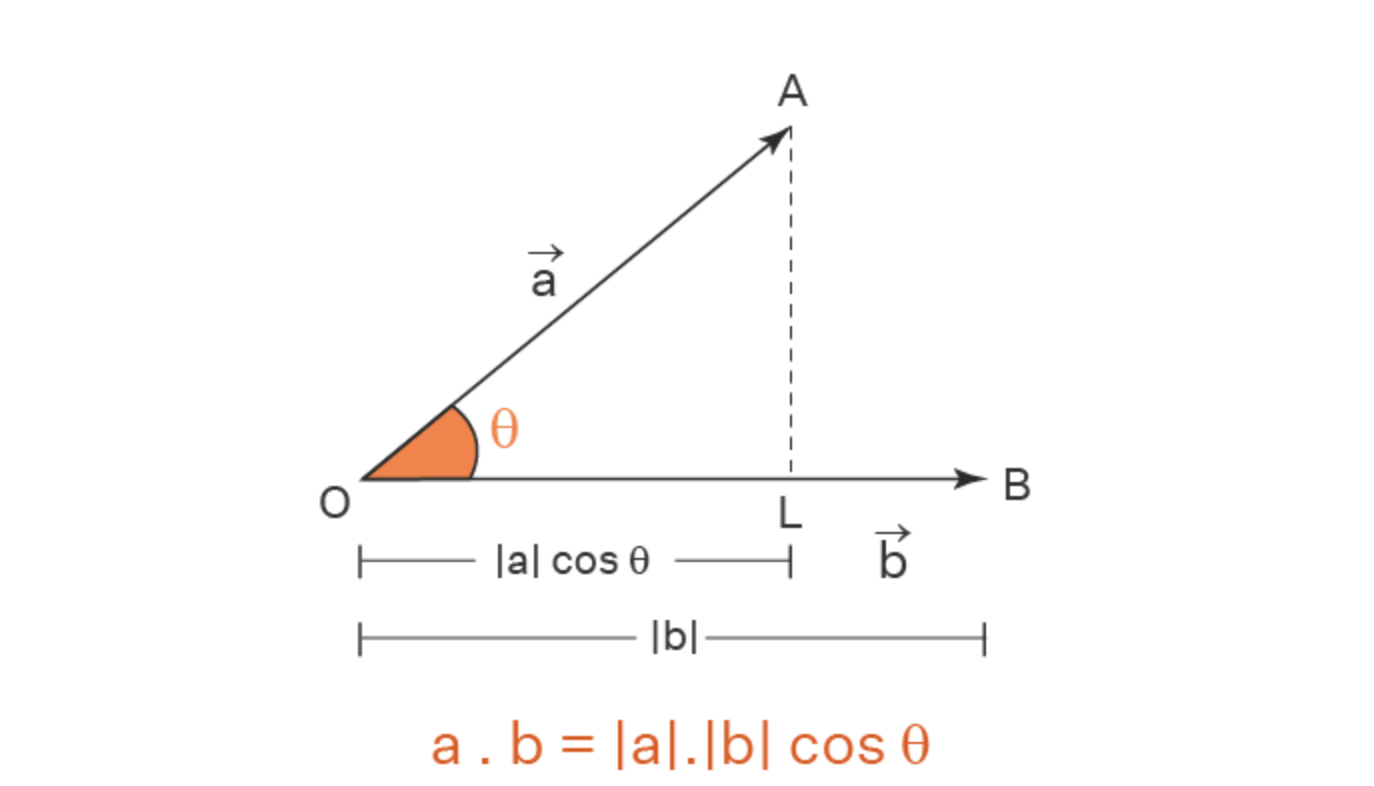
What is the Dot Product?

For two vectors $\mathbf{A}$ and $\mathbf{B}$, the dot product is defined as:
$$
\mathbf{A} \cdot \mathbf{B} = | \mathbf{A} | | \mathbf{B} | \cos(\theta)
$$
where:

• $| \mathbf{A} |$ and $| \mathbf{B} |$ are the magnitudes (lengths) of the vectors
• $| \mathbf{A} |$ and $| \mathbf{B} |$ are the magnitudes (lengths) of the vectors
• $\theta$ is the angle between them

Why is This Important in Word Embeddings?

• When $\theta$ is small, $\cos(\theta)$ is large, meaning the words are similar.
• When $\theta$ is large, $\cos(\theta)$ is small or negative, meaning the words are dissimilar.

Thus, in Word2Vec, the similarity between two words is determined by their dot product, which aligns with how we measure relationships in a semantic space.

---

Word2Vec: CBOW and Skip-Gram

Word2Vec is an algorithm for learning word embeddings. It has two main architectures:

1. Continuous Bag of Words (CBOW) – Predicts a word given its surrounding context.
2. Skip-Gram – Predicts context words given a target word.

CBOW Model

Given surrounding words, we predict the center word. The model uses:
$$
\mathbf{h} = \frac{1}{n} \sum_{i=1}^{n} \mathbf{x}_i
$$
where $\mathbf{x}_i$ are the input word vectors.

The probability of the target word $w_t$ is given by the Softmax function:
$$
P(w_t | \text{context}) = \frac{\exp(\mathbf{v_{w_t}} \cdot \mathbf{h})}{\sum_{w \in V} \exp(\mathbf{v_w} \cdot \mathbf{h})}
$$

Skip-Gram Model

Instead of predicting a word from its context, Skip-Gram predicts the context words given a target word:
$$
P(w_c | w_t) = \frac{\exp(\mathbf{v_{w_c}} \cdot \mathbf{v_{w_t}})}{\sum_{w \in V} \exp(\mathbf{v_w} \cdot \mathbf{v_{w_t}})}
$$

The loss function for Skip-Gram is:
$$
L = -\sum_{t} \sum_{-n \leq j \leq n, j \neq 0} \log P(w_{t+j} | w_t)
$$

---

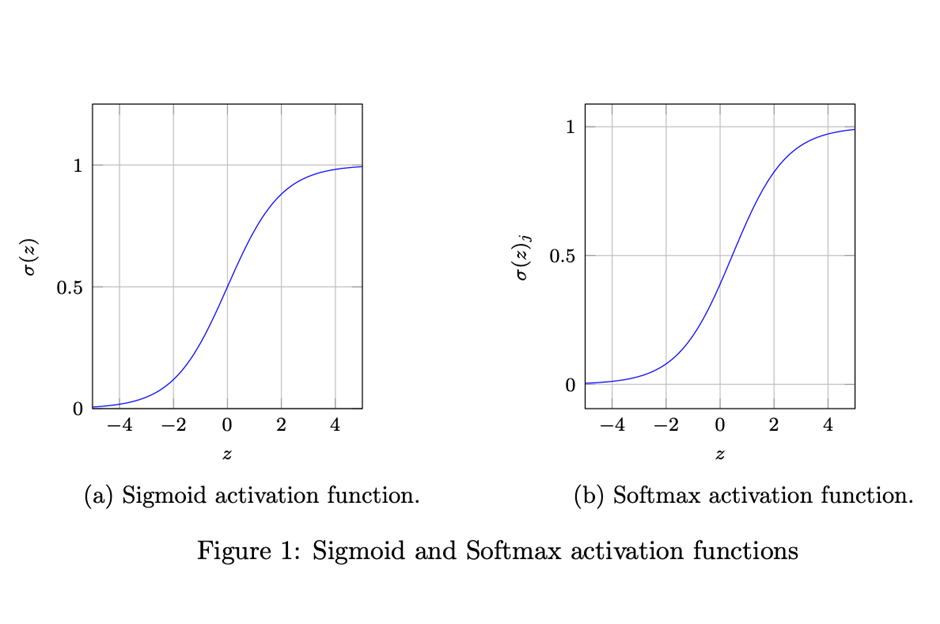
Understanding Softmax and Exponential Function

What is Softmax?

Softmax converts raw scores into probabilities. Given a vector $\mathbf{z}$, Softmax is defined as:
$$
\text{Softmax}(z_i) = \frac{\exp(z_i)}{\sum_{j} \exp(z_j)}
$$

This ensures:

• Non-negative outputs (since $\exp(x) > 0$ for all $x$).
• Probabilities sum to 1 (as a requirement for classification).

The exponential function $\exp(x) = e^x$ grows rapidly as $x$ increases. It is useful because:

• It ensures probabilities never become negative.
• It amplifies differences between scores, making classification more confident.

---

Negative Sampling: Efficient Training

Since computing Softmax over the entire vocabulary is expensive, we use Negative Sampling, which simplifies the loss function to:
$$
L = \log \sigma (\mathbf{v_{w_t}} \cdot \mathbf{v_{w_c}}) + \sum_{i=1}^{k} \log \sigma (-\mathbf{v_{w_t}} \cdot \mathbf{v_{w_{\text{neg}_i}}})
$$
where $\sigma(x) = \frac{1}{1 + e^{-x}}$ is the Sigmoid function.

Negative Sampling selects a few “negative examples” to contrast with positive word pairs, making training much faster.

---

Positional Encoding

In Transformer models, Positional Encoding is used to compensate for the lack of positional information in the self-attention mechanism. Since self-attention is order-agnostic, it does not inherently capture the sequence order, making it necessary to explicitly inject position information.

Why Do We Need Positional Encoding?

In sequential models like RNNs and LSTMs, inputs are processed step by step, inherently preserving order information. However, the Transformer model processes all tokens in parallel, making it unaware of the relative or absolute positions of words in a sequence. Positional Encoding helps encode positional information, ensuring the model can distinguish word order.

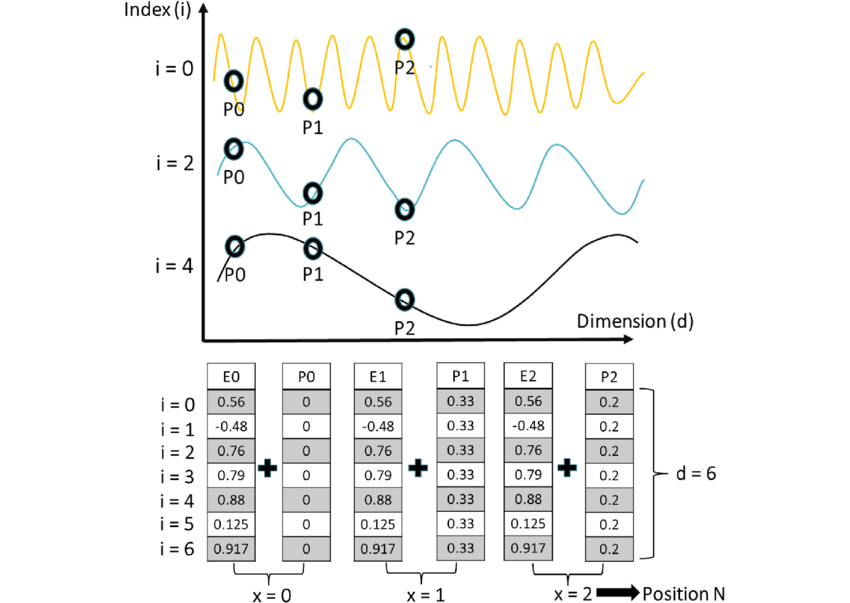
How Positional Encoding Works

The key idea of Positional Encoding is to generate a unique vector for each position in a sequence and add it to the corresponding word embedding. This allows the model to infer positional information.

Mathematical Formulation

The original Transformer paper Attention Is All You Need (Vaswani et al., 2017) defines positional encoding using sine and cosine functions:

$$
PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right)
$$

$$
PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{\frac{2i}{d_{\text{model}}}}}\right)
$$

Where:

• $pos$ represents the token position in the sequence.
• $i$ is the dimension index (even indices use sine, odd indices use cosine).
• $d_{\text{model}}$ is the embedding dimension, equal to the Transformer model’s hidden size.
• $10000$ is a scaling factor chosen empirically to spread the encoding values over different frequencies.

Why Use Sine and Cosine?

The choice of sine and cosine functions is motivated by several factors:

1. Periodicity: These functions provide a smooth, repeating pattern that captures relative positional relationships.
2. Smooth Transitions: The values change gradually as $pos$ increases, helping the model learn sequential dependencies.
3. Multi-Scale Representation: The denominator ensures different dimensions have different wavelengths, allowing the encoding to capture both local and global position information.