About Machine Learning ( Part 8: Convolution Neural Networks )

Convolutional Neural Networks (CNNs) have revolutionized the field of computer vision, enabling significant advancements in image recognition, object detection, and segmentation tasks. This blog will explore the key concepts behind CNNs and their working principles.

What is a CNN?

A Convolutional Neural Network (CNN) is a type of deep learning model specifically designed for processing structured grid data, such as images. Unlike traditional fully connected neural networks, CNNs leverage convolutional layers to capture spatial hierarchies in the data.

Architecture of a CNN

A typical CNN consists of the following layers: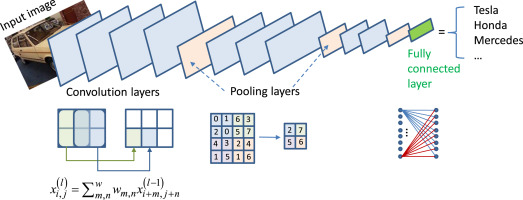

1. Convolutional Layer
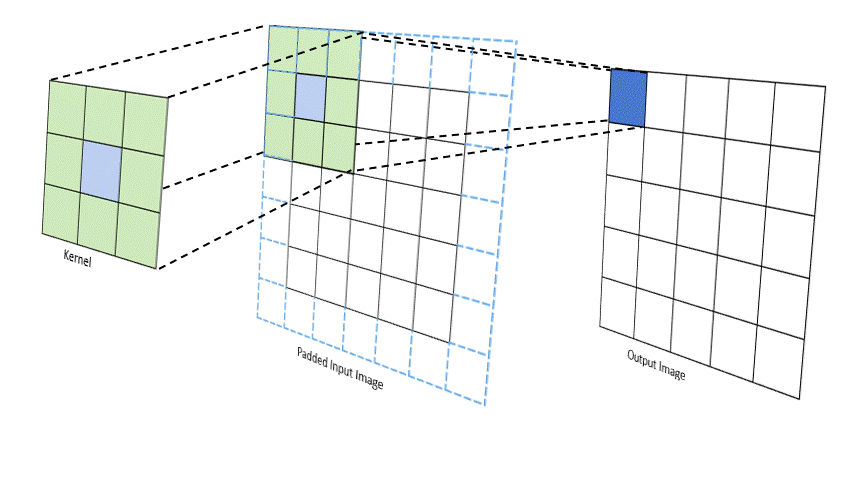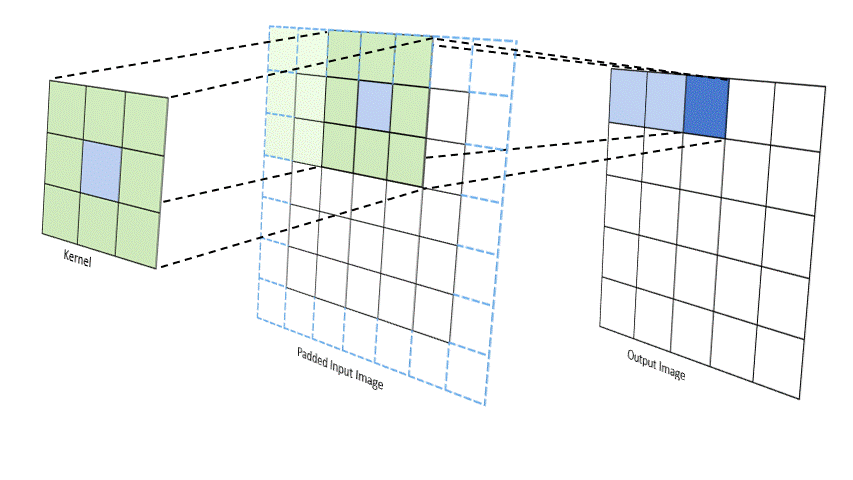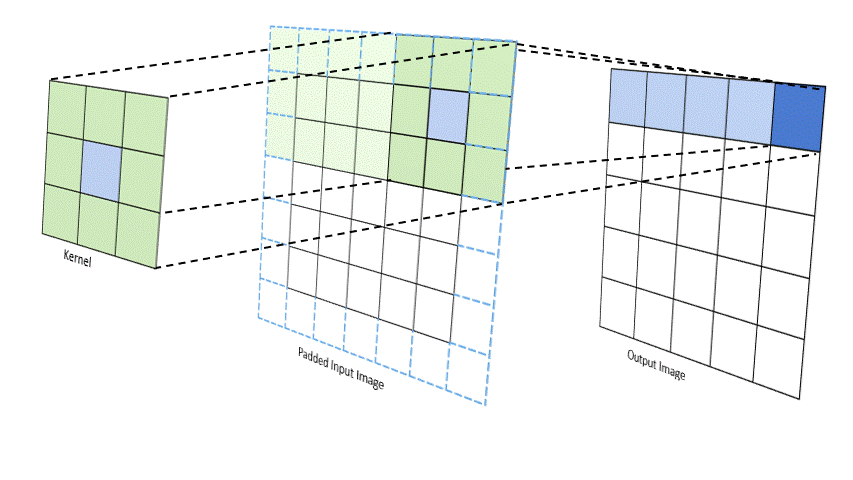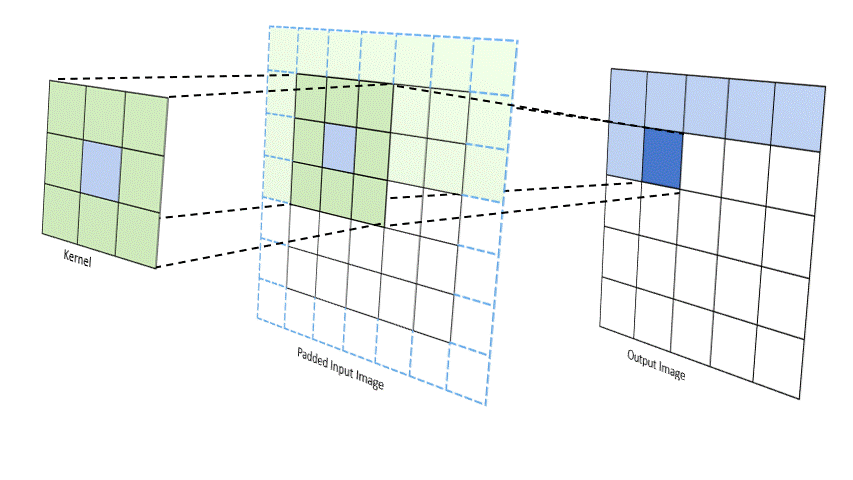
   The convolutional layer applies a set of learnable filters to the input image, extracting important features like edges, textures, and patterns. Mathematically, the convolution operation is defined as:

   $$ (I * K)(x, y) = \sum_{m}\sum_{n} I(m, n)K(x - m, y - n) $$

   where:

   • $I$ is the input image,
   • $K$ is the filter (kernel),
   • $(x, y)$ represents spatial coordinates.

2. Activation Function (ReLU)
   The Rectified Linear Unit (ReLU) introduces non-linearity into the model by applying:

   $$ f(x) = \max(0, x) $$

   This helps the network learn complex patterns.

3. Pooling Layer
   The pooling layer reduces the spatial dimensions of the feature maps, helping to decrease computational complexity. The most common type is max pooling:

   $$ P(x, y) = \max_{i, j} F(x+i, y+j) $$

   where $F(x, y)$ represents the feature map values.

4. Fully Connected Layer
   After several convolutional and pooling layers, the output is flattened and passed through fully connected layers to make final predictions.

Training a CNN

Training a CNN involves minimizing a loss function using an optimization algorithm like stochastic gradient descent (SGD). The loss function, often cross-entropy loss, is given by:

$$ L = -\sum_{i} y_i \log(\hat{y_i}) $$

where:

• $y_i$ is the true label,
• $\hat{y_i}$ is the predicted probability.

Backpropagation and gradient descent adjust the weights to minimize this loss iteratively.

Applications of CNNs

CNNs have a wide range of applications, including:

• Image Classification (e.g., recognizing objects in images)
• Object Detection (e.g., detecting pedestrians in autonomous driving)
• Medical Image Analysis (e.g., detecting tumors in X-rays)
• Facial Recognition (e.g., biometric authentication)